A1. 자기장에 의한 전하의 운동 ($\vec{E}=0$)

플라즈마는 양전하, 음전하로 가득찬 제4의 물질이다. 전기장은 전하를 가속시키고, 자기장은 전하를 회전시킨다. 전기장은 전하에 직접적으로 에너지를 주거나 뺏기 때문에 매우 직관적으로 이해할 수 있으나 자기장의 영향은 다소 이해하기 어렵다. 이번 글에서는 수식전개를 통해 자기장에 의한 전하의 운동을 알아본다.

(요구 배경지식: 일반물리, 대학수학)

(글 작성중 2021년부터 벡터가 수능에서 배제됐다는 걸 보고 적잖은 충격을 받았다...(⊙_⊙)???)

 

전하가 자기장을 지나게 되면, 속도와 자기장에 수직한 방향으로 힘을 받게 되는데 이를 Lorentz force라 부른다.

$$\vec{F}_B=q\vec{v}\times\vec{B}$$

Lorentz force는 전하에 구심력으로 작용하여 전하가 자기장을 중심으로 나선운동을 하게 한다. Lorentz force에 의한 나선운동을 제대로 이해하기 위해 원통 좌표계와 외적(cross product)을 짚고 넘어가보자.

---

A) 원통 좌표계 (Cylindrical coordinate)

직선 운동은 x,y,z 3축을 활용한 Cartesian 좌표계를 사용해 이해하는 것이 가장 좋다. 반면 회전 운동을 모사할 때는 원통 좌표계가 훨씬 더 유용하다. 아직 원통 좌표계가 익숙하지 않은 이학/공학도라면 이번 기회에 익혀보길 바란다.

 

Figure 1은 원통형 좌표계의 개념을 묘사한다. 먼저 2차원 평면에서 빨간 원을 따라 회전하는 물체 "P"를 들여다본다. 회전 반지름이 $r$을 갖는 P의 각도가 $\theta$인 순간, P를 향하는 단위벡터를 $\hat{r}$, 회전방향의 단위벡터를 $\hat{\theta}$라 한다. x축과 y축을 향하는 단위벡터 $\hat{x}$, $\hat{y}$는 불변하지만, $\hat{r}$과 $\hat{\theta}$는 $\theta$가 시시각각 바뀌기 때문에 회전과 함께 변하는 단위벡터로 OP의 벡터를 간결하게 묘사할 수 있다. 

여기서 z축을 추가해 3D로 옮긴 것이 원통형 좌표계로, 축대칭성을 갖는 현상이나 회전하는 물체를 묘사하는 데 있어 활용성이 높다.

 

Figure 1. 원통형 좌표계

 

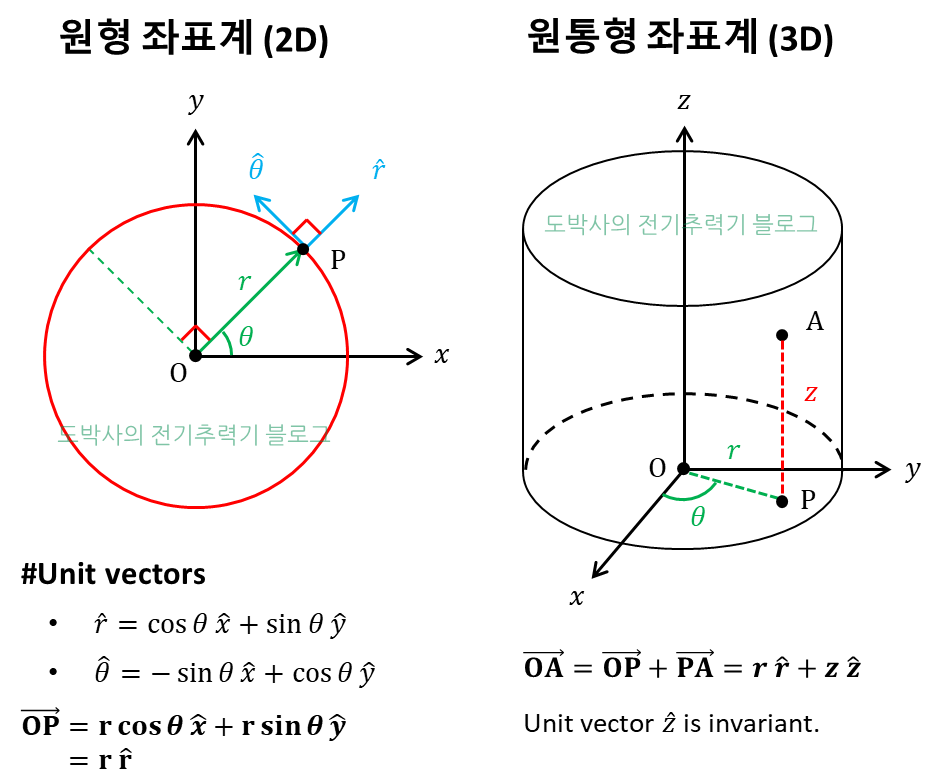
원통형 좌표계를 활용해 등속 원운동하는 물체 "P"의 운동방정식을 이해해보자.

원운동에서는 반지름이 변하지 않는다. 따라서 $\rm{\vec{OP}}$의 시간 미분, 즉, 속도는 다음과 같다.

$$\frac{d\vec{\rm{OP}}}{dt}=r\frac{d\hat{r}}{dt}=r\frac{d(\rm{cos}\theta\hat{\it{x}}+\rm{sin}\theta\hat{\it{y}})}{dt}=r\frac{d\theta}{dt}(-\rm{sin}\theta\hat{\it{x}}+\rm{cos}\theta\hat{\it{y}})=r\omega \; \hat{\theta}$$

(각속도 $\frac{d\theta}{dt}\equiv\omega$)

와 같이 표현된다. $\rm{\vec{OP}}$를 한번 더 미분, 즉, 가속도는 다음과 같다.

$$\frac{d^2\vec{\rm{OP}}}{dt^2}=r\omega\frac{d\hat{\theta}}{dt}=-r\omega^2 \; \hat{r}$$

가속도와 질량의 곱은 힘이다. 따라서 물체가 원운동하기 위해 필요한 힘, 즉, 구심력의 크기는 $-mr\omega^2$인 것이다.

 

B) 외적 (Cross product)

Figure 2는 벡터 사이의 연산, 내적과 외적을 설명한다.

 

먼저, $\vec{A}$와 $\vec{B}$의 내적은 |$\vec{A}$|와 $\vec{B}$가 가진 $\vec{A}$ 방향 성분의 곱과 같다.

반면, $\vec{A}$와 $\vec{B}$의 외적은 벡터를 결과물로 산출한다. 그 크기로는 |$\vec{A}$|와 $\vec{B}$가 가진 $\vec{A}$ 수직 성분의 곱이 되어  $\vec{A}$와 $\vec{B}$가 이루는 평행사변형의 넓이가 된다. 방향은 $\vec{A}$와 $\vec{B}$에 모두 수직인 방향이다. Figure 2를 보면 $\vec{A}$와 $\vec{B}$에 모두 수직인 방향은 위/아래 두 방향인데, 이는 오른손을 들어 확인하면 된다. 먼저 👉 모양을 취해 $\vec{A}$ 방향을 검지로 가리키고 검지손가락 꺾어 $\vec{B}$ 방향을 가리켰을 때 엄지손가락이 향하는 방향이 바로 외적의 방향이다. 외적은 곱하는 순서에 따라 산출되는 방향이 바뀌므로 순서에 유의해야 한다.

 

Figure 3. 내적과 외적

 

C) 자기장에 의한 나선운동

자기장에의한 나선운동을 설명하기 위해 먼 길을 돌아왔다. 이제 결실을 맺을 차례.

원통형 좌표계에서 자기장이 한 방향으로(편의상 $\hat{z}$) 균일하게 존재하는 환경에서 운동하는 전자를 떠올려보자. 그러면, 전자에 작용하는 Lorentz force는 다음과 같이 표현된다.

$$\vec{F}_B=-e \vec{v} \times B\hat{z}= eB \hat{z} \times \vec{v}$$

여기서 외적의 의미를 떠올려보면 Lorentz force를 이해할 수 있다. 먼저 자기장에 평행한 속도성분을 $\vec{v}_{\parallel}$, 수직 성분을 $\vec{v}_{\bot}$이라 정의하자. 그럼 자기장을 기준으로 속도를

$$\vec{v}=v_{\parallel}\hat{z}+v_{\bot}\hat{\theta}$$

와 같이 방향을 분리해 사용할 수 있다. 결과적으로 Lorentz force의 크기는,

$$\vec{F}_B=eBv_{\bot} \hat{z} \times \hat{\theta}=-eBv_{\bot} \hat{r}$$

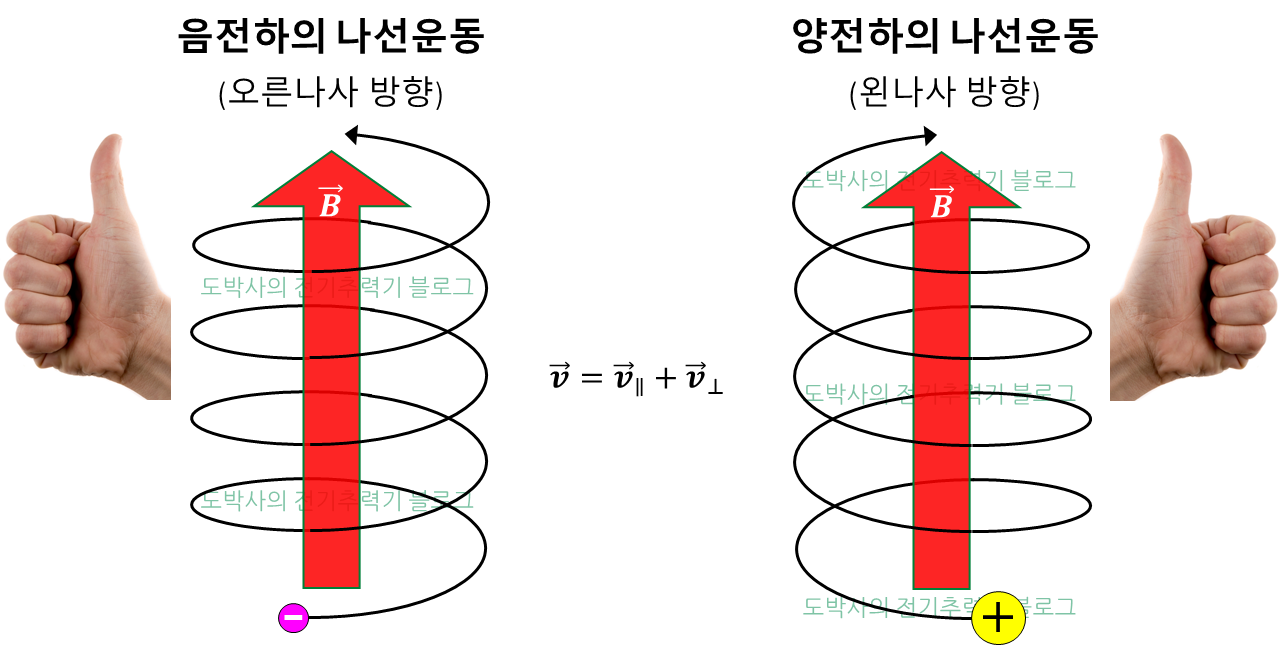
가 된다. $\vec{F}_B$의 방향은 $-\hat{r}$ 방향, 즉, 회전축을 향한다. 신경써서 물리공부를 했다면 눈치를 챌 수 있다. 원운동의 특징이란걸. Lorentz force는 전하에 구심력으로 작용하여 전자를 자기장을 기준으로 오른나사 방향으로, 양전하는 왼나사 방향으로 회전시킨다. (Figure 3 참고)

우리는 이러한 관계를 통해 자기장에 의한 전자의 각속도를 알 수 있다. ($\omega_{c}$: angular frequency of cyclotron motion)

$$ m r\omega_{c}^2 = eBv_{\bot} = eB\times r\omega_{c}$$

$$\therefore \omega_{c} =\frac{eB}{m}\;\;\; \rm{and} \it\;\;\;v_{\bot}=r\omega_{c} =\frac{eB}{m}r$$

자기장은 그에 수직성분에 해당하는 속도를 갖는 전하에 구심력을 가해 원운동하도록 한다. 반면 수평방향 성분에는 아무런 영향을 끼치지 않는다. 즉, $\vec{v}_{\parallel}$은 자기장과 관계없이 유지되는데, 이는 결과적으로 나선운동을 의미하며 전하의 나선운동 형상은 Fig. 3과 같고 속도는 아래와 같이 표현된다.

$$\vec{v}=v_{\parallel}\hat{z}+r\omega_{c} \hat{\theta}= v_{\parallel}\hat{z}+\frac{eBr}{m}\hat{\theta} $$

 

Figure 3. 자기장에 의한 전하의 나선운동