A2. E×B drift

이전 글에서는 자기장에 의한 전하의 운동을 들여다보았다. 블로그를 관심있게 볼 정도의 독자라면 전기장에 의한 전하의 운동은 이해하고 있을 터이니 생략하고, 이번 글에서는 전기장과 자기장이 모두 존재하는 환경에서 전하가 어떻게 움직이는지 알아본다.

(요구 배경지식: 일반물리, 대학수학)

---

1. 가정

• Static(일정한) 전기장과 자기장 ($\frac{\partial\vec{E}}{\partial t}=0$ and $\frac{\partial\vec{B}}{\partial t}=0$)
• Uniform(균일한) 전기장과 자기장. $\vec{E}=E_{\bot}\hat{y}+ E_{\parallel}\hat{z} $ and $\vec{B}=B\hat{z}$

---

2. E×B drift의 정량적 유도

전하의 운동을 이해하기 위해서는 운동방정식을 풀어야 한다. 전기장과 자기장이 주어진 환경에서 전하가 받는 힘은 다음과 같다.

$\vec{F}=q(\vec{E}+\vec{v}\times\vec{B}) = q(E_{\bot}\hat{y}+ E_{\parallel}\hat{z})+q\vec{v}\times\vec{B}$

$m(\dot{v_x}\hat{x} + \dot{v_y}\hat{y} + \dot{v_z}\hat{z} ) = q(E{\bot}\hat{y}+E_{\parallel}\hat{z}) + qB(v_y\hat{x}-v_x\hat{y}) $

 

위와 같이 얻은 운동방정식을 $\hat{x}$, $\hat{y}$, $\hat{z}$ term 별로 분리하면 다음과 같은 관계식을 얻게된다.

$\hat{x}\;\rm{term}:\;\it{} \dot{v_x}=\frac{qB}{m}v_y=\omega_c v_y$

$\hat{y} \;\rm{term}:\;\it{} \dot{v_y}=\frac{qE_{\bot}}{m}-\frac{qB}{m}v_x =\frac{qE_{\bot}}{m}-\omega_c v_x$

$\hat{z} \;\rm{term}:\;\it{} \dot{v_z}=\frac{qE_{\parallel}}{m}$

 

전하는 $\hat{z}$ 방향으로는 단순히 전기장을 따라 다음과 같이 일정하게 가속된다.

$(\rm{Result\;\it{v_z}})\; \it{v_z} = v_{\parallel \rm0}\rm+ \it\frac{qE_{\parallel}}{m}t$

반면, $\hat{x}$와 $\hat{y}$ 방향의 운동을 이해하려면 미분방정식을 풀어야 한다. 여기서 $\frac{qB}{m}$를 자기장에 의한 cyclotron angular frequency $\omega_c$로 줄여쓰고, $\hat{x}$ term에서의 방정식을 $\hat{y}$ term에 대입하면 아래와 같은 관계가 도출된다.

$\ddot{v_x}/\omega_c=\frac{qE_{\bot}}{m}-\omega_c v_x\;\;\; \rightarrow \;\;\; \ddot{v_x}+\omega_c^2 v_x = \omega_c^2 \frac{E_{\bot}}{B}$

 

대학수학을 했다면 미분방정식의 해가 다음과 같다는 걸 단박에 알 수 있다.

$(\rm{Result\;\it{v_x}})\it\;v_x = \frac{E_{\bot}}{B} \rm{+} \it{v_{\bot \rm0}} \sin\rm{(}\it{\omega_c t}\rm{+}\it{\phi}\rm{)}$

그리고 이렇게 얻은 $v_x$를 $\hat{x}$ term의 방정식에 대입하면 $v_y$를 얻을 수 있다.

$(\rm{Result\;\it{v_y}})\it\;v_y = v_{\bot \rm0} \cos\rm{(}\it\omega_c t\rm{+}\it{\phi}\rm{)} $

 

결과를 살펴보자. 자기장에 평행인 방향으로 전하의 운동에는 특이점이 없다. 반면, 자기장에 수직인 방향으로는 전기장이 없을 때와 비교해 자기장에 의한 원운동 성분에 $\hat{x}$ 방향으로 $\frac{E_{\bot}}{B}$ 만큼의 속도가 추가되었다. 이로부터 알 수 있는 E×B drift의 특이점은 두 가지를 꼽을 수 있겠다.

• E×B drift는 전하량, 질량과 무관하다.
• E×B drift는 전기장과 자기장 모두에 수직인 방향으로 발생한다.

결과적으로 E×B drift를 수식으로 표현하면 아래와 같다.

$$\vec{v}_{E\times B} = \frac{\vec{E}\times\vec{B}}{B^2}$$

 

3. E×B drift의 정성적 이해

자기장을 축으로 전하의 회전반경(r)은 전하의 수직방향 속력($v_{\bot}$)에 비례하는 현상을 통해 E×B drift를 이해해보자.

(2023.11.09 - [A. 플라즈마 배경지식] - A1. 자기장에 의한 전하의 운동 ($\vec{E}=0$) "C) 자기장에 의한 나선운동" 참고)

$$r\propto v_{\bot}$$

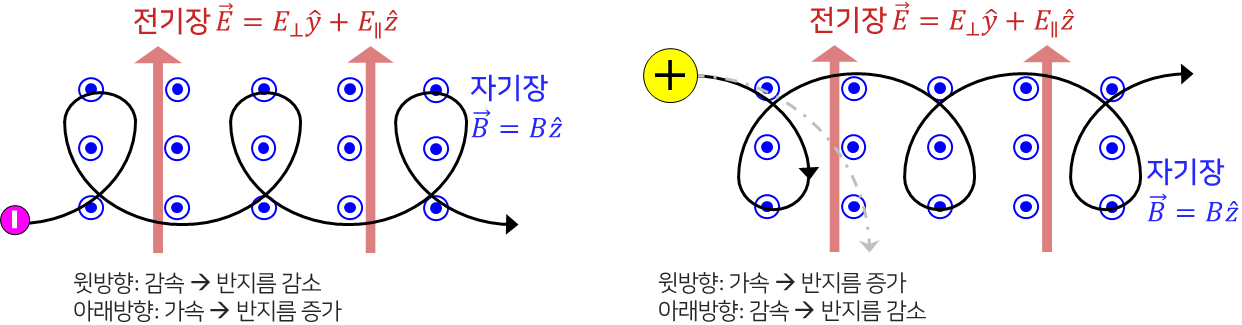
Figure 1은 음전하와 양전하가 균일한 전기장과 자기장이 존재하는 환경에서 어떤 경로로 운동하는지 나타낸다. 자기장을 기준으로 왼나사 방향으로 회전하는 양전하의 운동을 들여다보며 이해해보자.

위에서 보았듯 회전반경은 자기장 수직방향 속도의 크기에 비례한다. 양전하가 시계방향 12시에서 6시로 내려갈 때까지, 전기장은 양전하에게 $\hat{y}$ 방향으로 electrostatic force를 가하며, 이로 인해 양전하의 속도가 줄어들고 회전반경이 작아진다. (반대로 양전하가 6시에서 12시 방향으로 시계방향 운동을 할 때는 회전반경이 커진다.)

전기장이 없었다면 Fig. 1의 회색 점파선을 따라 원운동을 했을텐데, 양전하가 검정 실선을 따라 이동하는 것이다. 양전하의 평균적인 이동을 살펴보면 $\hat{x}$ 방향, 즉, 회전축이 전기장과 자기장에 수직인 방향으로 이동하는 것이다.

이러한 현상은 음전하에도 똑같이 나타나며 E×B drift 방향은 양전하와 동일하다.

Figure 1. 음전하와 양전하의 E×B drift 모사도