A3. Magnetic mirror

이전 글들을 통해 자기장이 균일한 환경에서 전하가 어떻게 움직이는지 살펴보았다.

1. 2023.11.09 - [A. 플라즈마 배경지식] - A1. 자기장에 의한 전하의 운동 ($\vec{E}=0$)
2. 2023.12.30 - [A. 플라즈마 배경지식] - A2. E×B drift

이번 글에서는 1번 상황에서 보다 깊이 파고들어 자기장 세기가 변하는 공간에서 높은 자기장 영역에서 전하가 반사되는 magnetic mirror 를 살펴본다.

이번 글까지 이해하면 오늘날 가장 인기있는 전기추력기인 홀추력기뿐 아니라 구동원리를 파악할 수 있으니, 좀 더 끈기를 내보자. (자기장이 중요한 이온추력기나 MPD 추력기를 이해하는 데도 필수적인 개념!)

(요구 배경지식: 일반물리, 대학수학)

---

1. 가정

• Static(일정한) 자기장 ($\frac{\partial\vec{B}}{\partial t}=0$)

---

2. Magnetic mirror effect의 정량적 유도

앞선 글들에서 보았듯, 전하의 속도 성분을 자기장에 평행한 방향과 수직인 방향으로 분리하여 해석하자.

$$\vec{v}=v_{\parallel}\hat{z}+v_{\bot}\hat{\theta}$$

$$W=\frac{m}{2}(v_{\parallel}^2+v_{\bot}^2)$$

고전역학에서는 뉴턴 방정식과 에너지($W$) 보존으로 물체의 운동을 설명할 수 있다. 자기장이 존재하는 플라즈마에서는 magnetic moment($\mu$) 보존 법칙이 물체의 운동에 관여한다.

$$\mu=\frac{mv_{\bot}^2}{2|B|}=\rm{invariant}$$

 

우리는 다음과 같이 에너지 보존식과 magnetic moment 보존식을 결합하여 자기장 세기($|B|$)가 세지면 전하의 수평방향 속도가 줄어듬을 알 수 있다.

$$W=\frac{mv_{\parallel}^2}{2}+\mu |B| \;\;\; \rightarrow \;\;\; \frac{mv_{\parallel}^2}{2} = W-\mu |B|$$

자기장은 전하에 에너지를 전달하지 않기 때문에 $W$는 고정된 값이다. 따라서 우리는 이 식에서 전하가 자기장이 세지는 영역을 지나면 $v_{\parallel}^2$이 줄어들고 결국 $v_{\parallel}=0$이 되는 순간이 올 수 있음을 알 수 있다. 다시 말해, 전하가 자기장이 센 영역을 통과하지 못하고 반사될 수 있다는 것인데, 이 현상을 magnetic mirror effect라 부른다.

 

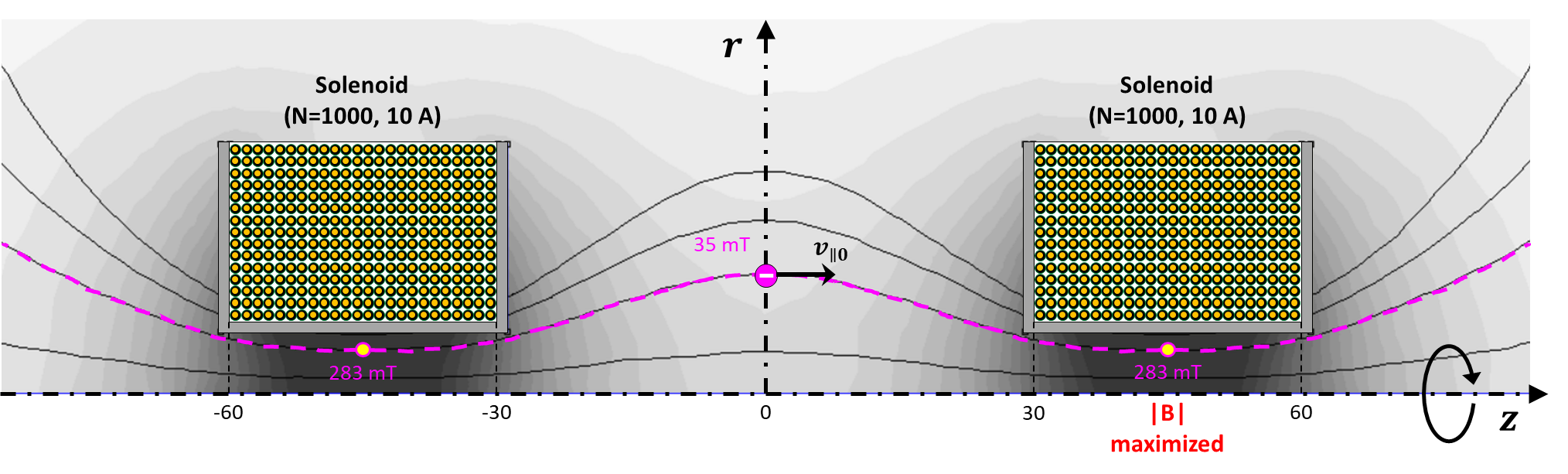
아래의 예시를 통해 magnetic mirror effect를 보다 면밀히 이해해보자. Figure 1은 평행하게 놓여진 솔레노이드 2개의 단면도로, 각 솔레노이드에 10 A의 전류가 인가된 상황에서 계산된 자기력선과 자기장 세기를 나타낸다. (솔레노이드 권선수: 1,000회) 솔레노이드의 중심부($z$ 축 위 $|z|$ ~ 45 mm 부근)에는 $z$ 방향으로 자기장이 균일하게 생성되는데, 솔레노이드로부터 벗어나면 자기장 세기가 약해지고 자기장 방향도 틀어진다. 자기력선을 따르는 전하의 나선운동을 기억하며(2023.11.09 - [A. 플라즈마 배경지식] - A1. 자기장에 의한 전하의 운동 ($\vec{E}=0$)) Fig. 1의 분홍색 자기력선 상에서 나선운동하는 전자를 살펴보자.

솔레노이드 사이에서 자기장이 가장 작은 곳은 $z=0$이다. $z=0$일 때 자기장 세기, 전자의 수평 및 수직방향 속도를 각각 $v_{\parallel 0}$, $v_{\bot 0}$, $B_0$라 하고 $\alpha = v_{\parallel 0}^2 /v_{\bot 0}^2$와 같이 변수 $\alpha$를 정의하자. 그러면 $v_{\parallel}$를 아래와 같이 전개할 수 있다.

$$\mu=\frac{mv_{\bot 0}^2}{2|B_0|} \;\;\; \& \;\;\;\; W=\frac{m v_{\bot 0}^2}{2} (1+\alpha) $$

$$\frac{mv_{\parallel}^2}{2} = \frac{m v_{\bot 0}^2}{2} (1+\alpha) - \frac{m v_{\bot 0}^2 }{2} \frac{|B|}{|B_0|} = \frac{m v_{\bot 0}^2}{2} (1+\alpha- \frac{|B|}{|B_0|})$$ 

잠깐, 우리는 여기서 $\frac{|B|}{|B_0|} = 1+\alpha$ 가 될 때 $v_{\parallel}=0$, 즉, 반사가 일어남을 알 수 있다. Figure 1의 분홍색 점선 상에서 $B_0 = 35 mT$, 자기장 최대값은 283 mT($\simeq 8B_0$)이다. 이는 $\alpha$ ≤ 7일 경우 magnetic mirror effect가 발동되어 전하가 두 솔레노이드 사이에 구속되고, $\alpha$ > 7 이라면 전하의 운동에 magnetic mirror effect가 발동되지 않고 자기력선을 따라 솔레노이드 사이를 유유히 빠져나감을 시사한다. 이와 같이 자기장이 최소화되는 지점에서 전하의 속도 성분비에 따라 magnetic mirror로 가둘 수 있음이 판가름되는데, 플라즈마 물리에서는 $\alpha$가 커서 가둘 수 없는 전하를 loss cone에 해당한다고 부른다.

Figure 1. Magnetic mirror 설명 예시. 평행하게 놓여진 솔레노이드 2개의 단면도. (검정 실선: 자기력선, 흑백명도: 자기장 세기)

---

Magnetic mirror effect는 자기장 세기의 변화가 클 때 유효한 현상이다. 자기장이 활용되는 전기추력기에서 magnetic mirror effect는 전자의 손실을 줄이는 막중한 역할을 한다. 다음 글에서는 실제 활용되는 홀추력기의 예시를 소개하여 그 중요성을 면밀히 파악해보자.